By Capt. Anthony Cowden, USN (ret.)
A recent article published by the Center for International Maritime Security (CIMSEC) – the first in a series – does an outstanding job of describing and explaining the Navy’s “core operating concept” of Distributed Maritime Operations (DMO). In short, DMO calls for “…the massing and convergence of fires from distributed forces, complicating adversary targeting and decision-making, and networking effects across platforms and domains.”1
The strike effectiveness of the DMO operating concept requires further investigation. In pursuing this, it is important to recall that a fleet does four things – it Scouts, it Screens, it Strikes, and it Bases.2 As currently envisioned, at least in open source definitions, DMO is not yet well-developed in the Scouting, Screening, and Basing functions of a fleet. Rather, DMO seems mostly focused on the offensive functions of a fleet, the Strike function.
The first step in this analysis will be to analyze a traditional concentrated force versus another concentrated force using the salvo equations. The second step will be to look at a distributed force that is able to mass fires against a concentrated force. The final step will be to look at a concentrated force that engages part of a distributed force. We will also look at what “firing effectively first” means in practice, and what happens if the enemy force distributes.
The Salvo Equations
The salvo equations were developed by the late Captain Wayne Hughes and are discussed in detail in Chapter 1 and Appendix A of Fighting the Fleet: Operational Art and Modern Fleet Combat. With the salvo equations, Captain Hughes showed:
“how modern naval combat follows a salvo model: opponents apply a pulse of combat power to each other in an instantaneous salvo exchange. A salvo exchange is an interaction of offensive combat power (e.g., mines, torpedoes, bombs, or missiles) and defensive combat power (e.g., surface-to-air missiles [SAMs], jamming, chaff, decoys). Combat power remaining from these interactions is applied against a target’s staying power (the number of hits of a particular weapon that a target can withstand and still be useful for combat purposes).”3
The salvo equations are presented here for reference:

Concentrated versus Concentrated
The first step in our analysis will be to look at two concentrated forces engaging one another. To simplify the analysis, it is assumed that each force is exactly equal, where each force consists entirely of the same number of missile-equipped surface ships, with the same offensive and defensive capabilities. These include:
- Each force consists of six surface ships (A = B = 6).
- Each surface ship has a displacement of 8,000 tons. Using the “cube root rule,” this means that it takes two “thousand-pound bomb equivalents” (TPBEs) to put a ship out of action. Given the destructive force of modern explosives, that equates to 2 x 660 lbs, or 1,320 lbs of modern warhead explosives. Assuming a warhead size of 500 lbs, it would take 2.64 warheads to put an 8,000 ton ship out of action. (a1 = b1 = 2.64).4
- Each surface ship is equipped as follows:
- Eight anti-ship cruise missiles (ASCMs) equipped with a 500 lb warhead. All ASCMs are considered to be “well-aimed” (i.e., unless otherwise destroyed, decoyed, or defeated, the ASCM would hit its intended target; this is not always true, as discussed in Chapter 1 of Fighting the Fleet.5 b = ).
- A surface-to-air missile (SAM) system capable of destroying two incoming ASCMs in a general engagement involving multiple incoming missiles.
- A close in weapons system (CIWS) capable of destroying two incoming ASCMs.
- An electronic countermeasure system (ECM) capable of defeating one ASCM.
- A decoy system capable of defeating one ASCM.
- Therefore, given the combined capabilities of the SAM, CIWS, ECM, and decoy systems to destroy or defeat incoming ASCMs, a3 = b3 = 6.
- Each force has equivalent organic and inorganic scouting capabilities, and is able to detect and localize the opposing force at the maximum range of their ASCMs.
Based on these assumptions, the salvo equations for an engagement between two concentrated forces are featured in Figure 1:

Predicting damage to warships in combat is always difficult, but a change in the number of units in force A and B () of 4.55 indicates enough hits to put 4.55 ships out of action in each force.6 Of course, this is highly dependent on hit distribution, which, if evenly distributed across the force, would mean that each ship in each force received some damage, but was not put out of action. In addition, this scenario assumes that each force was able to launch an attack “simultaneously,” where simultaneity is defined as each force being able to launch its ASCMs against the other force before it is hit by the other force’s ASCMs.
The essence of Captain Wayne Hughes’s admonition to “fire effectively first” then is to launch an attack and have missiles hit the opposing force before that force can launch its missiles.17 Assume that if force B was able to “fire effectively first,” then proceeding from the salvo equations above, force A would be reduced by a total of 4.55 ships, so force A’s subsequent attack on force B would result in the following:

A negative number for DB indicates that the B force is likely to be able to defeat all of force A’s incoming missiles; and the bigger the number, the more likely it will defeat the incoming strike. Such is the advantage of being able to “fire effectively first.”
This highlights two other aspects of offensive and defensive fires. First, close-range defensive fires such as point-defense missiles can often be replenished prior to another salvo attack. While they may be limited in their ability to defeat an incoming salvo, they can generally be reloaded and prepared to defend against a future salvo, without any reduction in capability. Second, this is not always true of ASCMs, many of which are housed in dedicated launchers and are limited in number and cannot be reloaded quickly or at sea. As the reader will see in this example, there is arguably little incentive to retain offensive fires for possible future engagements, as it often takes all the offensive firepower available to overcome the opponent’s defensive capability.
Distributed versus Concentrated
The second step in this analysis is to look at a distributed force that is able to mass its fires against a concentrated force. However, at this point the reader should be able to see that the results are likely to be similar as in the scenario presented above, assuming that the concentrated force is able to launch against all elements of the distributed force. An issue associated with the distributed force is the coordination required for a distributed force to mass its fires against a common target. Scouting information about target location, course, and speed would need to be communicated to all elements of the distributed force, and some sort of coordination and communication would need to occur for the distributed elements to mass their fires against the target. This is inherently more complex than attacking with a concentrated force, and more subject to communication and coordination failure.
The third step in this analysis is to look at a concentrated force that engages part of a distributed force. The danger in distributing one’s own force in the face of a competent – or lucky – opponent is that the opposing force will defeat one part of own force “in detail”; that is, the entire opposing force will engage just part of own force and be able to destroy it. Assuming that force A divides itself into two equal parts, A(1) and A(2), and assuming that force B engages A(1) before A(2) can become involved in the fight, such an engagement is characterized in the salvo equations as depicted in Figure 3:

Here we see that force B has a preponderance of offensive firepower that overwhelms A(1)’s defensive capability, and force B’s defensive capability is able to defeat force A(1)’s inadequate offensive punch. Should A(2) get off a shot against force B, its results would look exactly like those of force A(1), as shown in Figure 4:

The net result of the damage to force A in the distributed case would be the likely destruction of all three A(1) ships, with no damage to the opposing A(2) ships. Recall that in the concentrated case, the damage to force A ships (i.e., 4.55 put out of action) would be distributed over the six ships of the force. Here, however, enough offensive power from force B to put 11.36 ships out of action would only be distributed over the three ships of force A(1), virtually ensuring that all three ships would be put entirely out of action. Force B would not suffer any damage at all. Compare this to the concentrated case or the case where a distributed force A had been able to mass its fires (Figure 1), where force B would have suffered an equal amount of damage.
What happens if force B only detects one of the distributed parts of force A (force A(1)), but distributed force A is able to mass its fires against force B?
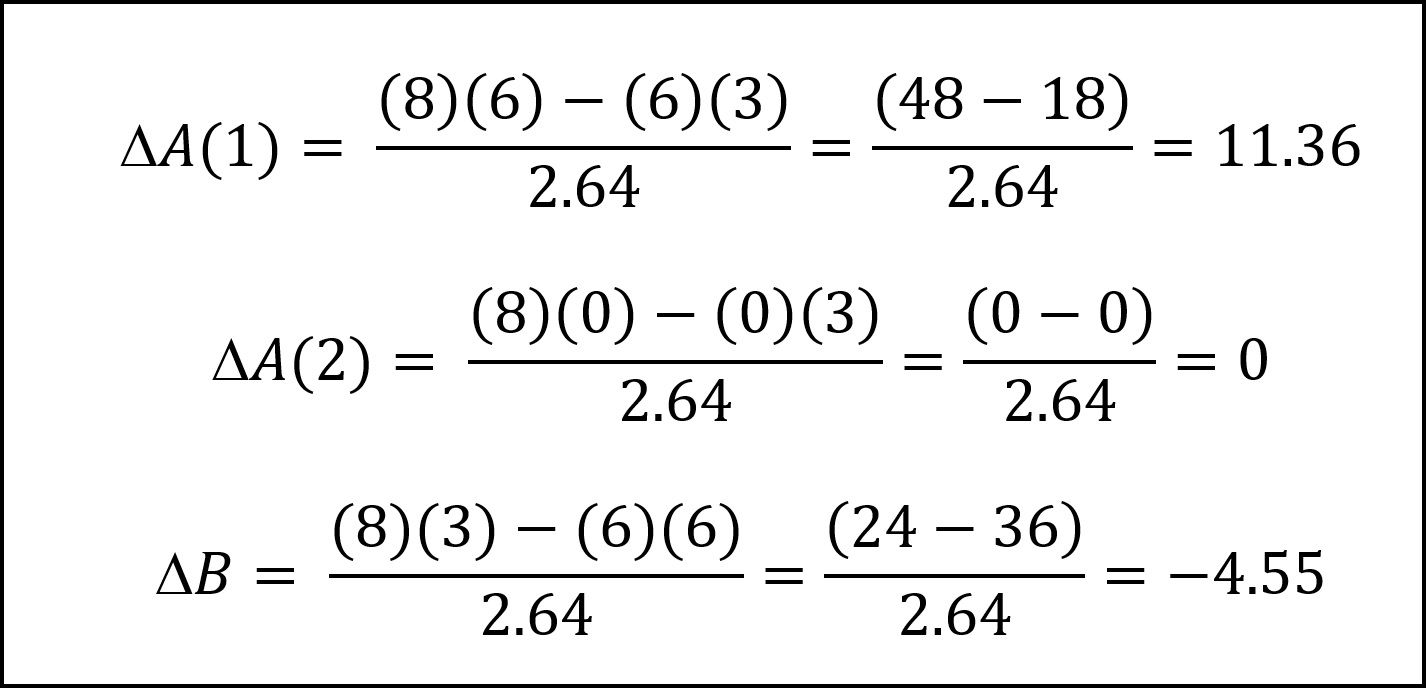
The result is depicted in Figure 5. All three ships of force A(1) would likely be put out of action, no damage would be incurred by force A(2), and force B would incur the same damage as if force A were concentrated. It turns out this is the one case where a distributed force has a strike advantage over a concentrated force. However, it should be noted that this is not an advantage conferred by distribution, it is an advantage conferred by effective Screening and Scouting. One part of the distributed force drew the attention and the fire of the concentrated force, but was able to combine its fires with the undetected portion of the distributed force.8
Next, what would happen if force B knew that force A had distributed itself, it had detected force A(1), and it assumed that force A(2) was nearby? If it retained half of its ASCMs for a possible future engagement with force A(2), the engagement with A(1) might look like the results contained in Figure 6:
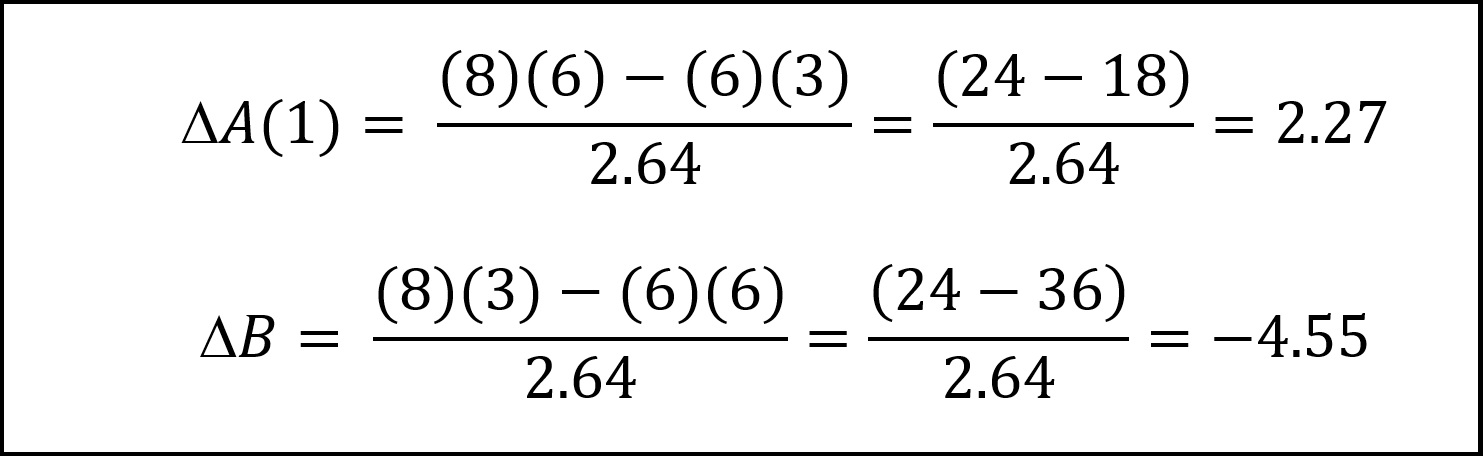
Of course, a future engagement with force A(2) would look much the same, and note that force B does not suffer any damage. Given the uncertainty of combat, it makes much more sense for force B to launch all of its ASCMs against force A(1), likely destroying all of force A(1), and use screening to scuttle back into port before any other force can attack it – a classic case of Corbett’s “arrested offense.”
“Fire Effectively First!”
In Figure 2, the value of firing effectively first was illustrated for the base case of two concentrated forces engaging one another. This also applies to a concentrated force and a distributed force that engage each other simultaneously. The following looks at the value of “firing effectively first” for two of the other cases discussed previously:
- A concentrated force that engages part of a distributed force (Figure 7). It should be self-evident that if the concentrated force, B, fires effectively first, the engaged part of the distributed force will be put out of action. But what happens if the part of the distributed force A(1) fires effectively first against the concentrated force B, and then B launches an attack on A(1)? As we can see in the following equations, B is able to defeat A(1)’s incoming salvo, and since it is undamaged, if it is able to launch an attack against A(1), it will overwhelm A(1)’s defenses.
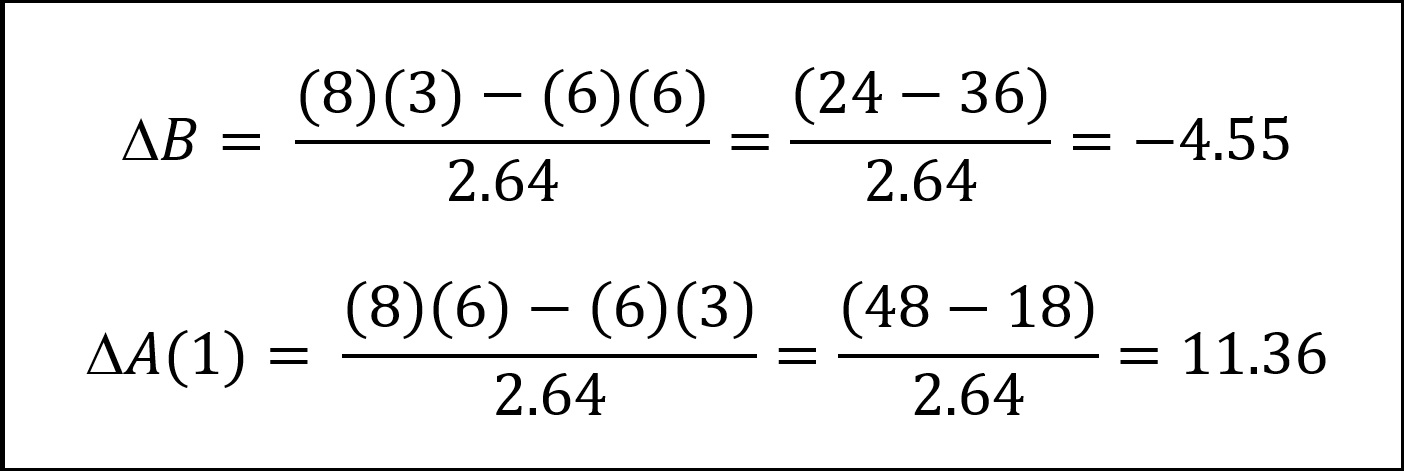
- A concentrated force only detects one of the distributed parts of force A (Figure 8). In this case, force B fires effectively first against force A(1), which is put out of action, and force A(2) launches a retaliatory strike against force B. A(1) is destroyed, and force B is able to defeat A(2)’s inadequate attack.
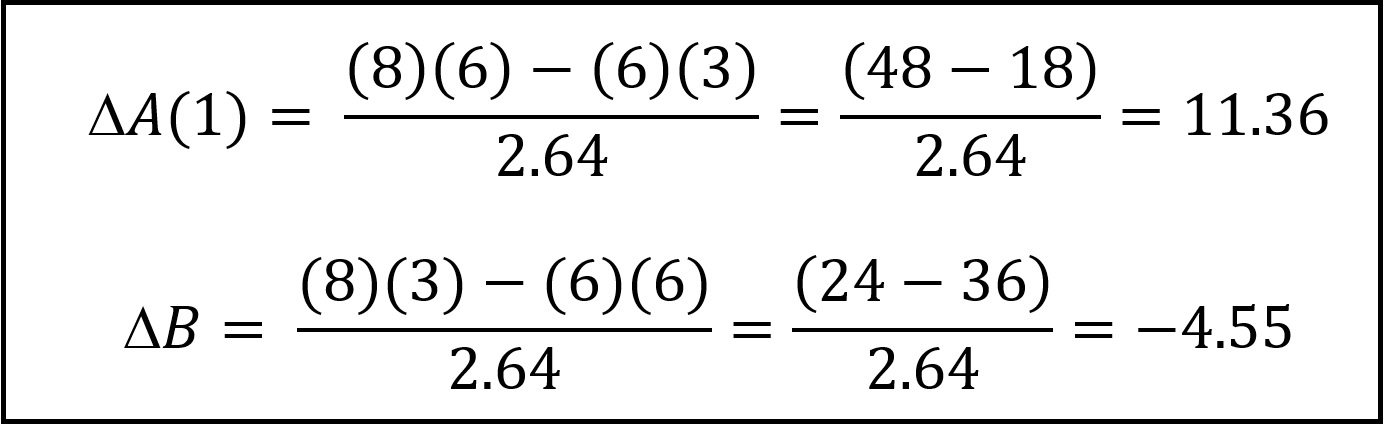
Whether a force distributes or not, what is essential to victory – and survival – is the ability to “fire effectively first,” and firing effectively first is a function of scouting, not distribution or concentration of platforms. That being said, even if the distributed force fires first, it will be unable to defeat or even damage the concentrated force unless it can effectively coordinate its attack.
What if the Enemy Distributes?
If distribution is a good idea, then we must expect the other side to distribute as well. The combinations of possible engagements begin to escalate quickly, depending on how each side distributes its forces. We can, however, look at some of the more interesting cases, based on the assumption that each side distributes evenly into two equally-sized groups of three ships:
- Both forces are able to launch coordinated attacks on each other near-simultaneously. The results will be the same as those depicted in Figure 1. Both sides being distributed provides no advantage to either side in terms of strike.
- One force is able to attack one part of the other force, but the entire other force is able to attack both parts of the first force. The results will be the same as those depicted in Figure 5. Both sides being distributed provides no advantage to either side in terms of strike.
These dynamics yield a set of recommendations, including:
- No matter how forces are deployed – concentrated, distributed, or some other way – win the scouting contest and “fire effectively first.”
- If forces are distributed but the communications capability is not able to coordinate their fires, then force posture must be rearranged to respect the limits of communication. If this cannot be done in time, then better to disengage to fight another day.
- Improve screening. Decoys, for example, can be very useful in diluting the effect of the enemy’s salvo. The effect of each ship in force A being able to decoy just one more missile each is shown in Figure 9: it effectively halves the amount of damage force A could expect to receive.
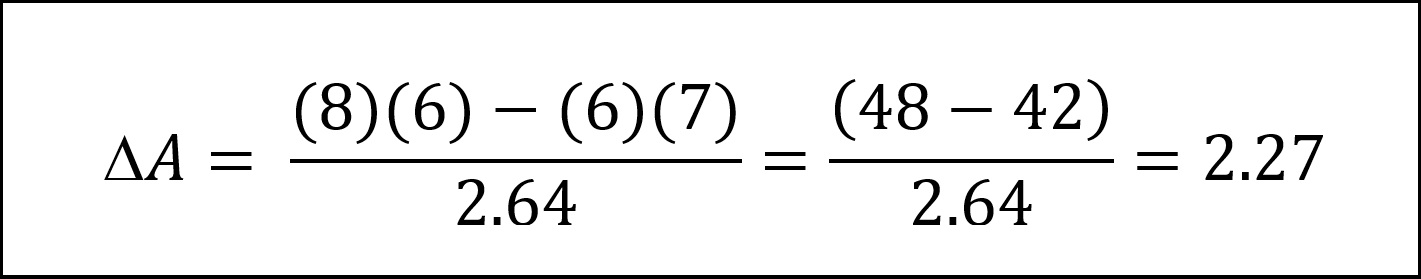
Conclusion
The salvo equations are analytical tools, not predictive ones. They do not result in “the answer” as to exactly how any single engagement will turn out. Combat entropy and instability, discussed at length in Fighting the Fleet, is a factor worth appreciating, such as how six bombs sunk four carriers at Midway, but five kamikazes did not sink one destroyer, USS Laffey, at Okinawa.9 That being said, the salvo equations can be used as an analytical tool to provide insight into probable outcomes. As they say, the race does not always go to the fastest, or the contest to the strongest, but that is the way to bet.
It should be noted that the single point of failure for a distributed force is the ability to coordinate a strike on another force. This coordination becomes even more complex with greater distribution of one’s own force, and even more so when the other force is distributed.10 If the distributed force cannot coordinate their fires then they lose in every scenario. This may be caused by jamming or some other interruption of communications, but it could also be from any failure to efficiently coordinate a strike, which could be as simple as poor distribution of weapons, training shortcomings, and other shortfalls.
The one case where a distributed force comes out ahead of a concentrated force is the case where only one part of the distributed force is detected by the enemy and absorbs the enemy’s attack, but is able to combine its strike with the other part of the distributed force before it dies. But that is not a “concept of operation,” it is more of a scouting tactic, and in prior generations this was better implemented with a LAMPS Mk III, Hawklink, and the naval tactical data system (NTDS).
DMO might be able to “complicate adversary targeting and decision-making” and it should be noted it would apply to one’s own force if the enemy distributes as well. But when it comes to the Strike function of a fleet, a distributed force had better be able to efficiently mass its offensive fires, or it runs the risk of being defeated in detail, resulting in, at best, a disappointing exchange in the number of destroyed and damaged ships.
Anthony Cowden is the Managing Director of Stari Consulting Services, co-author of Fighting the Fleet: Operational Art and Modern Fleet Combat, author of The Naval Institute Almanac of the U.S. Navy, has published numerous articles on a range of topics, and was a commissioned officer in the U.S. Navy for 37 years.
References
[1] Filipoff, Dmitry, Fighting DMO, Pt. 1: Defining Distributed Maritime Operations and the Future of Naval Warfare, Center for International Maritime Security, February 20, 2023, https://cimsec.org/fighting-dmo-pt-1-defining-distributed-maritime-operations-and-the-future-of-naval-warfare.
[2] Cares, Jeffrey R. and Anthony Cowden, Fighting the Fleet: Operational Art and Modern Fleet Combat (Annapolis, MD: Naval Institute Press, 2022), pp. 71-73
[3] Cares and Cowden, p. 16
[4] Cares and Cowden, p. 23. Estimating the number of hits to put a ship out of action is probably the most controversial aspect of using the Salvo Equations. The reader is invited to substitute whatever value they desire and conduct the analysis themselves. One useful approach is to use a parametric range of values and discover the sensitivity of the force to the number of hits required.
[5] Cares and Cowden, pp. 19-22
[6] How to interpret the Salvo Equations, as well as the concept of “Combat Entropy”, is discussed extensively in Chapter 1 of Fighting the Fleet.
[7] Hughes, Captain Wayne P., USN (Ret.) and Rear Admiral Robert P. Girrier, USN (Ret.), Fleet Tactics and Naval Operations, Third Edition (Annapolis, MD: Naval Institute Press, 2018), Chapter 13.
[8] Quick show of hands: who wants to serve in force A(1)?
[9] Cares and Cowden, pp. 19-22
[10] Distributed networked operations can become amazingly complex. Those interested in the theory and application of distributed network operations are invited to read Cares, Jeff. Distributed Network Operations: The Foundations of Network Centric Warfare. Newport, RI: Alidade Press, 2005.
Featured Image: Amphibious assault ship USS Bonhomme Richard (LHD 6) fires a NATO Sea Sparrow surface-to-air missile to intercept a remote-controlled drone as part of Valiant Shield 2016 (VS16). (U.S. Navy photo)


Enjoyed the article. One comment is offered.
As stated in the article: “The salvo equations assume each force has equivalent organic and inorganic scouting capabilities, and is able to detect and localize the opposing force at the maximum range of their ASCMs.” By extension, the equation then assumes that all of the missiles are “well-aimed”. The equation itself is a useful representation of the relationships of the various factors that affect salvo computations, except for the key factors of scouting and anti-scouting that directly affect the lethal and hard-to-find tenets of DMO respectively. Perhaps it is time for the formulation of a “Scouting Equation” that identifies the factors and relationships involved in scouting and anti-scouting that need to be incorporated in the salvo equation to capture the full range of factors that have to be considered in future analyses. For instance, what happens when the salvo equation incorporates the number of missiles not “well-aimed”, e.g. affected by anti-scouting measures, or not launched for lack of timely target tracking.
Thank you, some great observations!
We discuss the “not well-aimed” concern, as well as the fact that some defense will be wasted on these missiles, among other things, in our discussion of Combat Entropy in “Fighting the Fleet” (all royalties go to NMCRS!):
https://www.usni.org/press/books/fighting-fleet
This article is very interesting but the main question I am curious about is a bit elsewhere. It is not only about the same number of vessels – just in two or in one group. It is also about smaller number of big warships vs. bigger number of small warships. In other words, the same payload (mainly missiles in this case) but divided between more hulls. For example, six 8000t hulls vs. nine 6000t hulls. Do you know similar simulations with such parameters?
A great question! The Salvo Equations are quite easy to use, so I invite to you to plug in the numbers you present and give it a whirl! Please let us know what you discover. I would suggest, however, that you start with the same number of large vessels vs. the same number of smaller vessels (there are all sorts of small missile boats, much smaller than 6000t, that can carry the same number of ASCMs as, say, a DDG). That will illuminate the effect of size alone – then you can expand it from there.